Definition and Understanding of e Number

Image From http://www.gogeometry.com/

e number is a number that is the base of natural logarithms. There are several ways of defining it. Probably the most satisfactory is this. First, define natural logarithms (ln) as in approach 2 to the logarithmic function. Then define exponential (exp) as the inverse function of ln in exponential function. Then define e as equal to exp 1. This amounts to saying that e is the number that makes

It is necessary to go on to show that and exp x are equal and so are identical as functions, and also that ln and  are identical functions.

The number e has important properties derived from some of the properties of ln and exp. For example,

Also, e is the sum of the series

Another approach, but not a recommended one, is to make of one these properties the definition of e. Then exp x would be defined as 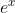 and exp x, ln x would be defined as its inverse function, and the properties of these functions would have to be proved.

The value of e is 2.718 281 83 (to 8 decimal places). The proof that e is irrational is comparatively easy. In 1873, Hermite proved that e is transcendental, and his proof was subsequently simplified by Hilbert.